Pythonでの主成分分析の実施方法と用途を考える

データサイエンス課、ブログ担当です。
今回は、統計手法の一つである主成分分析について、Pythonで実施してみました!
この記事によってわかること
- Pythonを用いた主成分分析の実施方法がわかる。
- 主成分分析の具体的なイメージがつく
- 主成分分析が有効かどうかを判断できるようになる
複数の変数がある場合、見比べながら解析しなくてはならず、解釈が非常に大変です。
そのため変数を減らすことができる主成分分析を実際に触って、使用感を試してみました。
(この記事では実施方法に焦点を当てています、数式等を用いた詳しい原理等は参考文献にまとめておきます。)
使用するデータはPythonのscikit-learnで準備されている、カリフォルニア州の住宅データセットを用いました。
主成分分析(PCA)とは
主成分分析(PCA)は多変量解析の一つで、
変数が多いデータの情報を損なわずに次元削減(変数を減らす)を行うという統計的な手法です。
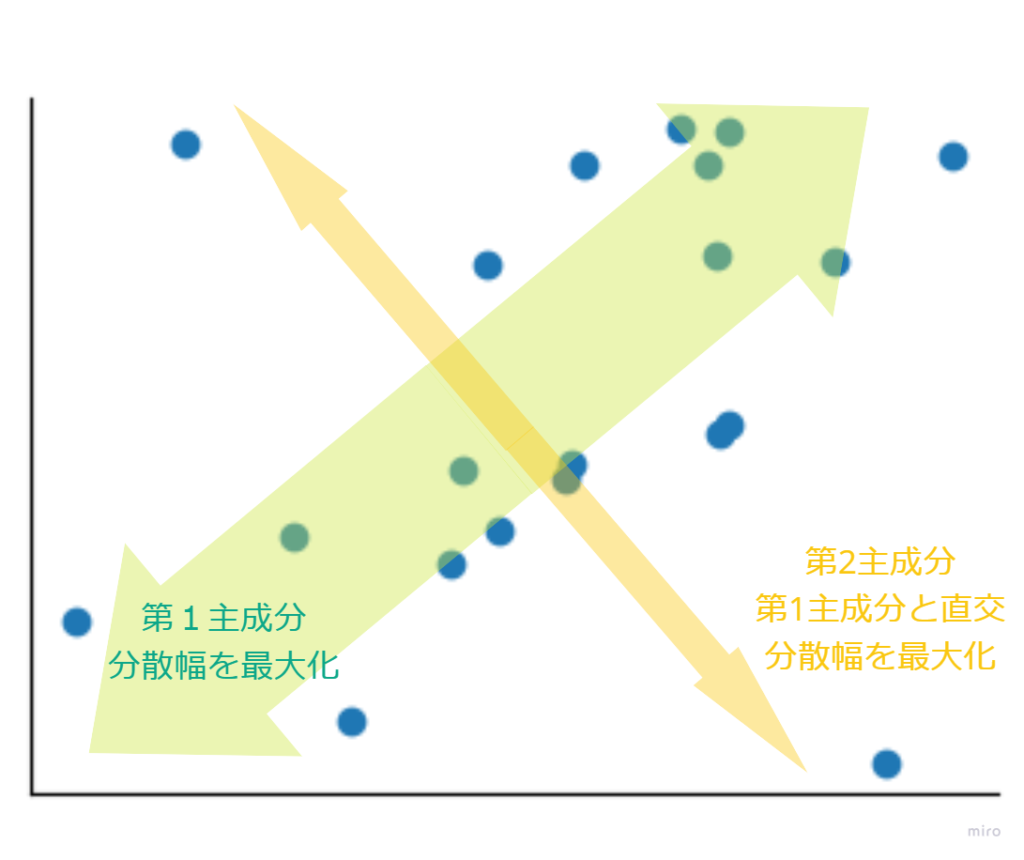
主成分分析ではデータの分散が最大化するように変数(主成分といいます)を作成するため、情報が集約されます。
作成した主成分と直角に交わる方向で、分散が最大になる主成分を新たに作成していくというアルゴリズムになっています。これにより第1主成分>第2主成分>…というように情報の量が集約されていきます。
上記のアルゴリズムにより、相関係数が高い変数を集約することで、変数の数を減らすことができます。
主成分分析で重要な概念
1,固有値
固有値の大小によって、主成分が持つ情報の量や重要度が表されています。
そのため固有値が大きい場合は、元の変数のデータをよく反映していると考えられます。
2,寄与率
寄与率は固有値をすべての固有値の合計で割って計算しており、主成分が元の全データをどれだけ反映しているかを割合で表しています。また、ある主成分までの寄与率の合計値を累積寄与率といい、70~80%程度になるまでの主成分を選択するといいと考えられています。
3,因子負荷量
主成分分析の結果、新しい変数(主成分)が作成されますが、その主成分が何の指標になっているのかということは出力されません。そのため主成分の持つ意味を解釈するために因子負荷量という指標を使用します。因子負荷量は主成分と元の各変数との相関係数で計算しています。これにより元の変数とどれだけ関連しているか(元の変数の情報が集約されているか)が判断できます。
※より詳しい原理がわかる参考文献
使用するデータセット概要
| 変数名 | 本記事では以下のように略記 | 説明 |
|---|---|---|
| MedInc | 収入 | ブロックでの収入の中央値 |
| HouseAge | 築年数 | ブロックでの住宅の築年数の中央値 |
| AveRooms | 部屋数 | ブロックでの平均部屋数 |
| AveBedrms | 寝室数 | ブロックでの平均寝室数 |
| Population | 人口 | ブロックでの人口 |
| AveOccup | 世帯人数 | 平均世帯人数 |
| Latitude | 緯度 | ブロックでの緯度(値が大きいほど北) |
| Longitude | 経度 | ブロックでの経度(値が大きいほど東) |
| Price | 住宅価格 | 住宅価格(目的変数として格納) |
実装方法
実装準備
Pythonで主成分分析を実行するにあたり、必要なライブラリやデータセットを準備します。
ライブラリの準備
# 必要なライブラリのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import matplotlib.ticker as ticker
import seaborn as sns
from sklearn.datasets import fetch_california_housing
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
# .ipynbのファイル形式を使用しているとき、グラフをアウトプット行に表示できる
%matplotlib inline主成分分析を行うにあたり、必要なモジュールをインポートします。
データセットの読み込み
準備されているカリフォルニア州の住宅データセットを読み込みます。
またカラム名を日本語の略記に変更します。
# データセットのクラスをインスタンス化→DataFrameに格納
Housing = fetch_california_housing()
columns_jap = ["収入", "築年数", "部屋数", "寝室数", "人口", "世帯人数", "緯度", "経度"] # 変更先のカラム
df_data = pd.DataFrame(Housing.data, columns=columns_jap) # 目的変数のデータ
df_target = pd.DataFrame(Housing.target, columns=["住宅価格"]) # 説明変数("Price")のデータ
housing_df = pd.concat([df_data, df_target], axis=1, sort=False)データセットの前処理
カリフォルニア州の住宅データセットについて、
下記の記事を参考にしてデータの前処理(外れ値の除去)を行います。
参考 【Qiita】scikit-learn カリフォルニア住宅価格データの前処理に関する見解
# データの前処理(外れ値の除去)
housing_df = housing_df[housing_df["部屋数"] < 100]
housing_df = housing_df[housing_df["人口"] < 20000]
housing_df = housing_df[housing_df["世帯人数"] < 200]
housing_df = housing_df[housing_df["築年数"] != 52]
housing_df = housing_df[housing_df["住宅価格"] < 5.00001]データセットの確認
主成分分析を実施する前に、データセットの中身を簡単に分析してみます。
相関係数マップの図示
まずはデータセットの列ごとの相関係数を確認して、データの傾向を分析してみましょう。
# フォントを日本語対応のものに変更
plt.rcParams['font.sans-serif'] = ['MS Mincho']
# 各データ同士の相関係数を一覧で表示
plt.figure(figsize=(11, 7))
sns.heatmap(cbar=False, annot=True, data=housing_df.corr()*100, cmap="coolwarm")
# plt.title("% Correlation Map", fontname="MS Gothic")
plt.title("相関係数マップ [%]")
plt.show()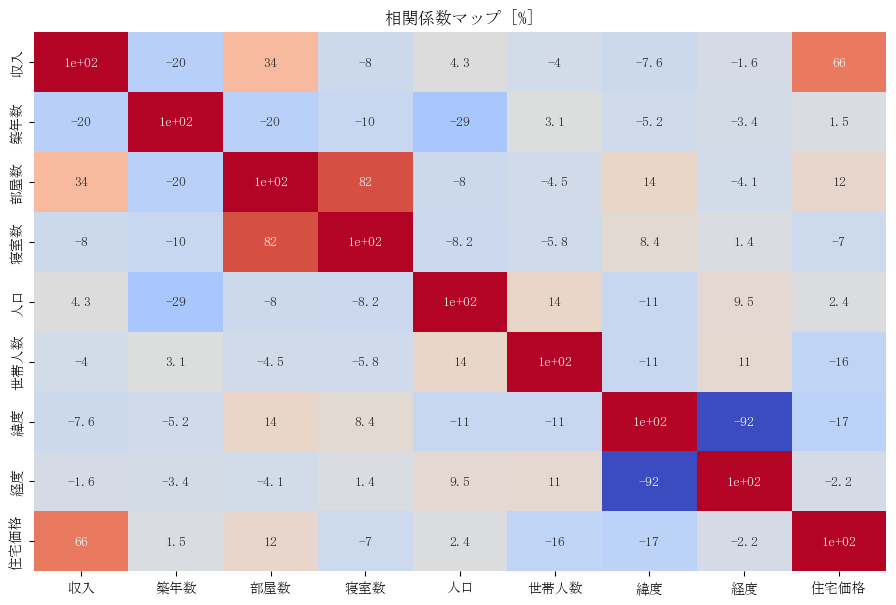
こちらを参考にして”MS Mincho”の部分を日本語対応のフォントに変更してください。。
“findfont: Generic family ‘sans-serif’ not found because none of the following families were found: MS Mincho”
上図ではデータセットの行ごとの相関係数をマップ化しており、正の相関係数が大きいほど赤色に、負の
相関係数が大きいほど青色に表示されています。
ここで上図で相関係数を確認すると、緯度と経度は-92、部屋数と寝室数は82、収入と住宅価格は66というように、3組のデータに強い相関があります。
また収入と部屋数は34、人口と築年数は-29といった2組に弱い相関があります。
散布図の作成
まずは地理関係から分析してみましょう。
以下のコードによって、緯度と経度の関係を表示してみます。
# 緯度の値で並び替える
sorted_housing_df = housing_df.sort_values(by="緯度").copy()
# 緯度についてカラーバーを設定
norm = colors.Normalize(
vmin=sorted_housing_df["緯度"].min(),
vmax=sorted_housing_df["緯度"].max()
)
# LatitudeとLongitudeの散布図を作成
plt.figure(figsize=(10, 6))
scatter = plt.scatter(
x=sorted_housing_df["経度"],
y=sorted_housing_df["緯度"],
c=sorted_housing_df["緯度"],
cmap="viridis",
norm=norm
)
plt.colorbar(scatter, label="緯度")
plt.xlabel("経度")
plt.ylabel("緯度")
plt.grid(True)
plt.show()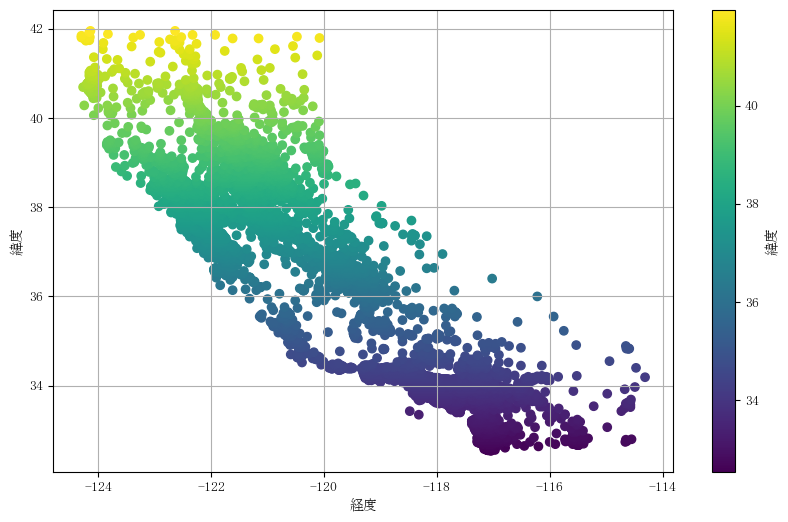
上の散布図では、横軸を経度(値が大きいほど東)、縦軸に緯度(値が大きいほど北)をとっており、
なおかつ緯度の値が大きいほど(場所が北に位置するほど)黄色に、値が小さいほど(場所が南に位置するほど)紫色になるようにカラーバーを設定しています。
ここで、Google Mapよりカリフォルニア州の地図を確認してみます。
なお赤色の点線でカリフォルニア州を囲んでいます。

先ほどの散布図はカリフォルニア州の地図と同じような形になっているため、データを調査したブロックの位置を示していることがわかります。
ここで先ほどの緯度に関するカラーバーを用いて、相関係数が高い他の組み合わせについても確認してみます。
(コードはほとんど同じのため省略)


左図が部屋数(横軸)と寝室数(縦軸)、右図が収入(横軸)と住宅価格(縦軸)に関する散布図になります。
また各データについて、北になるほど黄色、南になるほど紫色になるカラーバーを用いて、散布図のデータを色分けしています。
2つの散布図を取得してみると、黄色のデータが散布図全体の左下に偏っていることから、北部(北西部)のほうが、部屋数と寝室数は少なく、収入と住宅価格が低い傾向がありそうです。
主成分分析の実装
いよいよこのデータセットに対して、主成分分析を行っていきましょう。
データの標準化
まずは変数同士の比較を行えるようにするため、データの標準化を行います。
# データを標準化
Std = StandardScaler()
data_std = Std.fit_transform(housing_df)主成分分析の実行
標準化したデータに対して主成分分析(PCA)を行います。
Pythonには有名な分析手法が実施しやすいようにライブラリが準備されているため、
下記のコードで簡単に主成分分析が実施できます。
# 主成分分析を実施
Pca = PCA()
Pca.fit(data_std)
feature = Pca.transform(data_std)累積寄与率の出力
上記のコードで分析は完了です。主成分分析の結果を確認してみましょう。
まずは累積寄与率を確認します。第n主成分をPCnとしてラベリングします。
# 累積寄与率のグラフを作成
plt.gca().get_xaxis().set_major_locator(ticker.MaxNLocator(integer=True))
plt.plot([0] + list(np.cumsum(Pca.explained_variance_ratio_)), "-o")
plt.xlabel("主成分数")
plt.ylabel("累積寄与率")
plt.grid()
plt.show()
# 累積寄与率の値を表示
ccr_df = pd.DataFrame(
Pca.explained_variance_ratio_.cumsum(),
index=[f"PC{x+1}" for x in range(9)],
columns=["累積寄与率"]
)
print(ccr_df)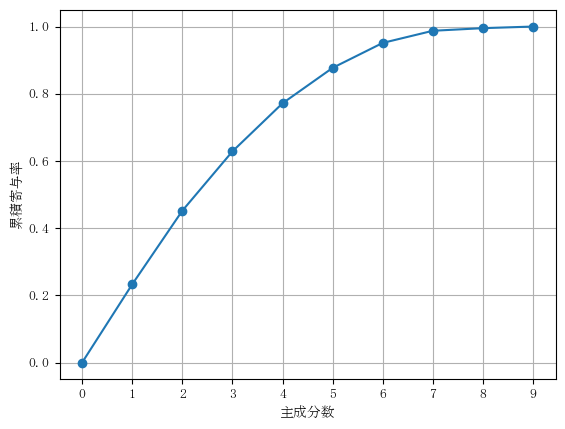
累積寄与率
PC1 0.232835
PC2 0.451871
PC3 0.628409
PC4 0.771574
PC5 0.877030
PC6 0.951292
PC7 0.987410
PC8 0.995205
PC9 1.000000
この累積寄与率を確認すると、PC4までで約77%のため、第4主成分までを採用すればいいことがわかります。
今回は第4主成分まで採用して分析を行っていきます。
因子負荷量の出力
主成分分析結果を解釈するため、因子負荷量を出力します。
今回は第4主成分まで選択するため、下記のコードのように記述します。
# 因子負荷量を求める
loading_num = 4
loading = pd.DataFrame(
Pca.components_[:loading_num],
columns=sorted_housing_df.columns,
index=[f"PC{i+1}" for i in range(4)]
)
loading = loading.round(2) # 小数点第2位まで表示
print(loading)出力結果:
収入 築年数 部屋数 寝室数 人口 世帯人数 緯度 経度 住宅価格
PC1 0.19 -0.15 0.51 0.43 -0.13 -0.18 0.48 -0.45 0.10
PC2 0.47 -0.22 0.34 0.20 0.14 -0.01 -0.45 0.42 0.42
PC3 -0.45 -0.04 0.31 0.53 -0.03 0.17 -0.17 0.32 -0.51
PC4 0.02 -0.61 -0.05 -0.10 0.68 0.28 0.17 -0.12 -0.18
なお出力結果については、インデントがずれていため、調整して表示しています。
因子負荷量の分析
今回作成した主成分に対して、簡単な解釈を行います。
ではもう一度、先ほどの因子負荷量の表を表示してみましょう。
出力結果:
収入 築年数 部屋数 寝室数 人口 世帯人数 緯度 経度 住宅価格
PC1 0.19 -0.15 0.51 0.43 -0.13 -0.18 0.48 -0.45 0.10
PC2 0.47 -0.22 0.34 0.20 0.14 -0.01 -0.45 0.42 0.42
PC3 -0.45 -0.04 0.31 0.53 -0.03 0.17 -0.17 0.32 -0.51
PC4 0.02 -0.61 -0.05 -0.10 0.68 0.28 0.17 -0.12 -0.18
因子負荷量は値の絶対値が1に近いほど、元の変数をよく反映していることを表します。
上の表では出力結果に対して、因子負荷量が大きい数字を太文字で記載しています。
ここで結果を簡単に分析してみます。
PC1とPC2は両方とも位置情報(緯度と経度)を多く含んでいます。
さらに、PC1については部屋数と寝室数の情報量が多いため住宅の密集具合を、PC2については年収や住宅価格の情報量を多く含んでいるため、地価が高い地域かどうかを表していると仮説を立てることができます。
これは主成分分析の原理によるもので、
分散が最大化するように新たな変数(主成分)を作成するため、
同じような傾向(相関)を持っている別のデータの情報を新たな変数にまとめることができます。
これが主成分分析を実施することにより、変数の数が減らせる理由です。
ただ新しく作成する主成分については、分析者本人が解釈を実施しなければならないため、
慣れが必要そうですね…。
主成分分析を適用する判断基準
ここで、主成分分析を行うかどうかを判断する際の判断基準として、元の変数と相関がある変数が多いかどうかが考えられそうです。
分散を最大化するように変数を再設定する方法のため、相関係数が高い変数はまとめて新しい変数にすることで変数の数を減らすということが主成分分析の要所っぽいです。
(主成分は直角に交わる方向で作成しているため、主成分同士は無相関になっています。)
今回の実施例で考えると緯度と経度、部屋数と寝室数、収入と住宅価格は高い相関を示していました。
そのため主成分分析によって変数の数が9個から4個に減らすことができたと考えられます。
主成分分析を行うかどうかの判断材料として、相関係数を取ってみると見込みがありそうかを判定できそうです。
では実際に相関係数の大小が次元を削減する判断基準になるかどうかを検証してみましょう。
無相関のデータの作成
データ同士が無相関であるデータを作成するために、ランダムなデータを用いてデータを作成しましょう。
新にrandomモジュールをインポートして、ランダムなデータを作成します。
import random
# ランダムなデータのシード値を固定
np.random.seed(123)
n = 10000
# ランダムなデータを作成
random_array = []
for i in range(9):
data = np.random.rand(n).tolist()
random_array.append(data)相関係数マップの図示
作成したデータをDataFrameにして、相関係数マップを確認してみます。
# 作成したデータをPandasに変換
random_df = pd.DataFrame(random_array)
random_T_df = random_df.T
random_T_df.columns = [f"PC{x+1}" for x in range(9)]
# 散布図を描画
plt.figure(figsize=(11, 7))
sns.heatmap(cbar=False, annot=True, data=random_T_df.corr()*100, cmap="coolwarm")
plt.title("相関係数マップ [%]")
plt.show()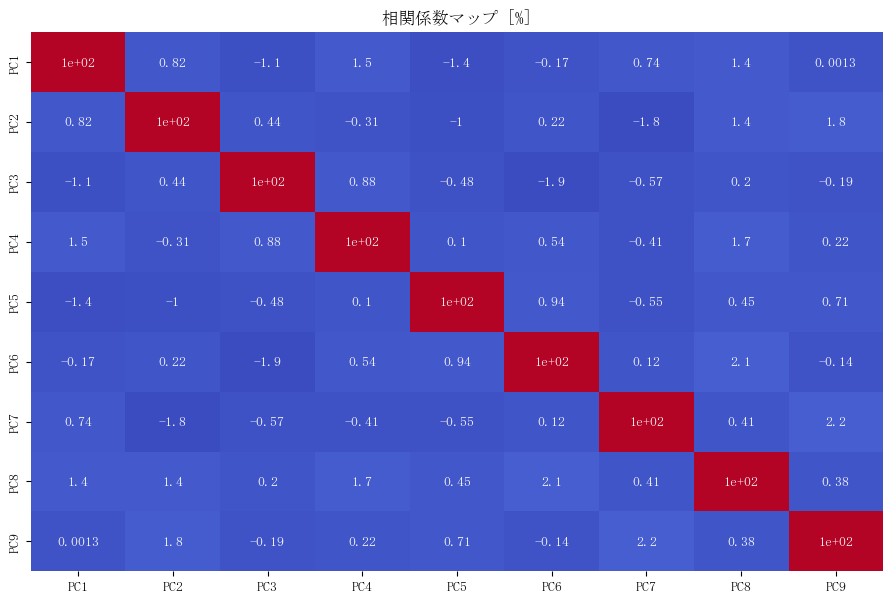
上記の図を確認すると、データ間の相関係数は非常に低く、
狙い通り無相関に近いデータを作成することができました。
主成分分析の適用と累積寄与率の出力
ではいよいよ作成したデータに主成分分析を適用し、累積寄与率を出力してみます。
# 主成分分析を実施
Pca2 = PCA()
Pca2.fit(np.transpose(random_array)) # 転置を実施
feature2 = Pca2.transform(np.transpose(random_array))
# 累積寄与率のグラフを作成
plt.gca().get_xaxis().set_major_locator(ticker.MaxNLocator(integer=True))
plt.plot([0] + list(np.cumsum(Pca2.explained_variance_ratio_)), "-o")
plt.xlabel("主成分数")
plt.ylabel("累積寄与率")
plt.grid()
plt.show()
# 累積寄与率の値を表示
ccr2_df = pd.DataFrame(
Pca2.explained_variance_ratio_.cumsum(),
index=[f"PC{x+1}" for x in range(9)],
columns=["累積寄与率"] )
print(ccr2_df)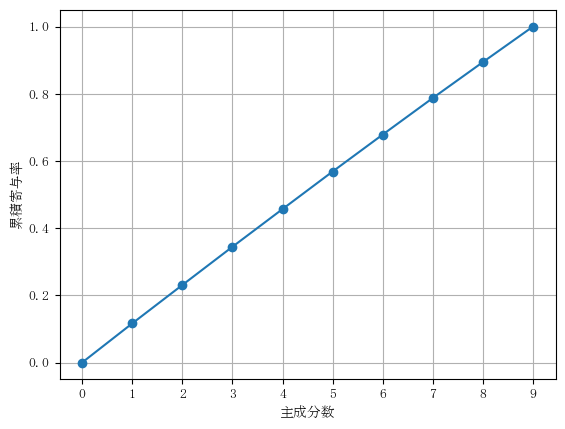
累積寄与率
PC1 0.116430
PC2 0.230729
PC3 0.344511
PC4 0.456750
PC5 0.568515
PC6 0.678495
PC7 0.787378
PC8 0.894250
PC9 1.000000
上記のグラフを確認すると直線になっており、各主成分の寄与率がほぼ等しい(情報を新たな主成分に集約できていない)ことがわかります。
以上よりデータ同士の相関が強い場合には有効な手法であると言えます。
本記事のまとめ
以下に今回の検証で得られた知見をまとめます。
- 主成分分析の実施時のコードをまとめた。
- 取得したデータの相関係数を取り、高い相関を確認できているなら主成分分析を実施する価値がある。
また別の機会にも技術を深堀りした記事を投稿する予定ですので、ぜひお見逃しなく!!
参考文献
主成分分析の原理
カリフォルニアデータセット詳細
・ 【Qiita】scikit-learn カリフォルニア住宅価格データの前処理に関する見解





